المستقيم ،نصف مستقيم ، قطعة مستقيمة

المستقيم :

•  المستقيم الذي يشمل النقطتين A و B، وهو غير محدود من الجهتين ، فيمكننا تمديده بالمسطرة من الجهتين.
•   نرمز إلى المستقيم الذي يشمل النقطتين A و B بالرمز (AB) أو بالرمز (d) ونقرأ المستقيم d 
• نعين نقطتين A و B ثم نرسم خط يشملهما باستعمال المسطرة . كما هو موضح في الشكل التالي: 

 نصف المستقيم :

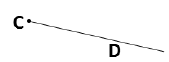
•  نصف المستقيم الذي مبدؤه C ويشمل النقطة D، وهو محدود من جهة C وغير محدود من جهة D، فيمكننا تمديده بالمسطرة من جهة D فقط . 
•  نرمز لنصف المستقيم هذا بالرمز [CD) . 

الشكل التالي يمثل نصف المستقيم [CD). 

القطعة المستقيمة :

•  قطعة مستقيمة طرفاها النقطتان E و F وهي محدودة من الجهتين بطرفيها نرمز لها بالرمز [EF] ونرسمها كما في الشكل التالي 

 طول قطعة مستقيمة : 

•  طول قطعة متسقيمة طرفاها النقطتان E و F، وهو عدد ،  مثال قطعة مستقيمة طولها 3سم يكتب EF=3cm .
•  تكون نقط في استقامية إذا انتمت إلى مستقيم واحد. 

مثال : 

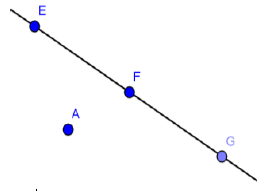
النقط E، F، G في استقامية . نكتب : `E in (FG)` نقرأ النقطة E تنتمي إلى المستقيم `(FG)` وكذلك : `G in (EF)` و `F in (GF)` 

النقط A، E، G ليست على استقامية نكتب : `A notin (EG)` نقرأ : النقطة A لا تنتمي إلى المستقيم `(EG)`. وكذلك : `E notin (AE)` و `G notin (AG)`

مستقيمات متوازية ، مستقيمان متعامدان ، استقامية نقط:

• المستقيمان المتوازيان هما مستقيمان غير متقاطعان .
•  المستقيمان المتطابقان هما مستقيمان  متوازيان.

مثال :

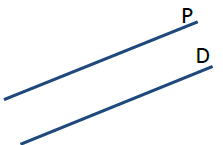
 `(P)` و `(D)` مستقيمان متوازيان لانهما لا يلتقيان في نقطة ونكتب $(D) \parallel  (P)$

 `(F)` و  `(G)` مستقيمان متوازيان لأنهما منطبقان ونكتب :   $(F) \parallel (G)$

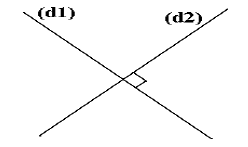
•  المستقيمان المتعامدان هما مستقيمان متقاطعان ويشكلان زاوية قائمة.

مثال : 

نكتب (d2) ⊥ (d1)  نقرأ المستقيم (d1) عمودي على  المستقيم (d2)

ملاحظة:

 تكون النقط في استقامية إذا  كانت تنتمي إلى نفس المستقيم.

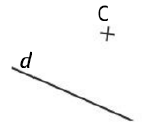
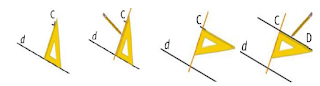
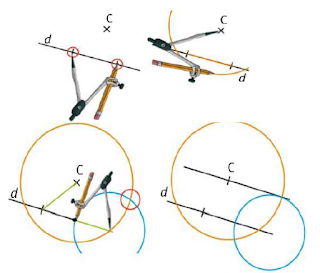
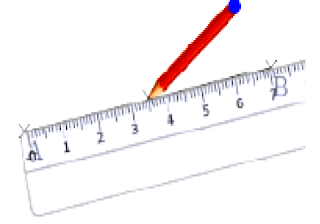
• لرسم مستقيم يوازي d و يشمل النقطة c نستعمل طريقتان:

1. الطريقة الأولى باستعمال الكوس:

الطريقة الثانية باستعمال المدور 

منتصف قطعة مستقيمة 

منتصف قطعة مستقيم هو نقطة من هذه القطعة متساوية البعد عن طرفيها
مثال :النقطة `M` منتصف قطعة المستقيم `[AB]` معناه: `M ∈[AB]` و `AM = BM`

طرق تعيين منتصف قطعة مستقيم:

1 . القياس بالمسطرة وأخذ نصف الطول.

2 . الورق الشفاف ثم الطي حتي يتطابق طرفا القطعة وأثر الطي على القطعة هو منتصفها