لمعرفة ما هي الدالة نعرض المثال التالي ، نفرض أن في الفاتح من شهر جانفي كان لذيك 100 دينار، وفي الأيام الموالية أصبح أباك يمنحك 50 دينار كل يوم ، إذا كنت تحافظ على كل المال الذي تحصل عليه، فكم سيصبح عندك بعد 10 أيام؟.
سيصبح عندك حتما 100+50×10 أي 600 دينار
إذا رمزنا لعدد الأيام بالرمز `x` والمبلغ المحصل عليه بالرمز `y` فإنه يمكننا أن نكتب : `y=50x+100` أي أننا عبرنا عن المبلغ الذي يمكن أن نجمعه بدلالة عدد الأيام مضروب في مبلغ الإدخار اليومي مضاف إليه المبلغ المحصل عليه سابقا.
I- تعريف ومصطلحات
- الدالة ببساطة هي العبارة التي ترفق بكل عدد `x` صورة له `y`
- نرمز للدوال بالرمز `f(x) ` ، `g(x) ` ، `h(x)` ، .... الخ
- نسمي `f(x)` أو `y` حيث : `f(x)=y` الدالة أو الصورة أو الترتيبة
- يسمى `x` المتغير أو السابقة أو الفاصلة
- كل دالة معرفة على مجال يسمى مجموعة التعريف `D`
* ملاحظة هامة :
يمكن للصورة أن يكون لها عدة سوابق لكن العكس غير صحيح للسابقة صورة وحيدة فقط
II- طرق تعريف الدوال
1- دالة معرفة بدستور
مثال : `f(x)=x^2+2x +1`
- مجموعة تعريف الدالة `f` هي :
`D_f=mathbb(R)=]- infty ; +infty[`
- صورة العدد 3 بالدالة `f` هي : `f(3)=3^2+2(3)+1 =16`
- سوابق العدد 1 بالدالة `f` هي `f(x)=1` أي :
`x^2+2x+1=1 Rightarrow `
`x^2+2x=0 Rightarrow`
` x(x+2)=0 Rightarrow`
` x=0` أو `x=-2`
2 - دالة معرفة بتمثيل بياني :
مثال : الشكل المقابل يمثل تمثيل بياني لدالة `g`
- مجموعة تعريف الدالة `g` هي : `D_g=]-3;3[`
- صورة العدد 1 بالدالة `g` هي 3 وصورة 0 هي 4
- سوابق العدد 3 بالدالة `g` هي 1 و `-1` وسوابق 0 هي 2 و `-2`
- العدد 5 ليس له سوابق بالدالة `g`
3- دالة معرفة بجدول تغيرات
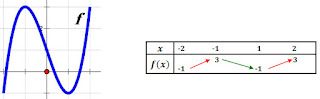
مثال : الجدول المقابل يمثل جدول تغيرات لدالة `h`
- مجموعة تعريف الدالة `h` هي `D_h=[0;+infty[`
- صورة العدد 0 بالدالة `h` هي 0 وصورة 4 هي 2
- سابقة العدد 3 بالدالة `h` هي 9
- العدد `-1` ليس له سوابق بالدالة `h`
4- دالة معرفة بجدول قيم
مثال : يمثل الجدول المقابل تعريفات بريد الجزائر لسنة 2005، إذا رمزنا للطرود البريدية بالدالة `h` فإن :
- مجموعة تعريف الدالة `h` هي : `D_h=]0;30]`
- صورة 12 بالدالة `h` هي 62
- سوابق 83 هي كل الأعداد من المجال `]15;20]`
- العدد 70 ليس له سوابق بالدالة `h`
III- التمثيل البياني لدالة :
- التمثيل البياني أو المنحنى الممثل للدالة في المعلم $(O;\overrightarrow{ I};\overrightarrow{J})$ هو مجموعة النقط `M(x;y)` حيث : `y=f(x)` و `x in D_f`
- نرمز إلى منحنى الدالة `f` بالرمز `C_f`
- نقول أن `y=f(x)` هي معادلة `C_f` في المعلم $(O;\overrightarrow{ I};\overrightarrow{J})$
تنبيه وملاحظة هامة :
ما عدا الدوال الخطية، التآلفية والثابتة لا يمكن رسم أي دالة أخرى عن طريق الجدول المساعد أو النقاط المساعدة لأنه هناك العديد من الكيفيات للمرور من نقطة إلى أخرى فمن الضروري أن تعطى معلومات أخرى حول سلوك الدالة وسنتعلم في محور الدوال المرجعية إحدى الطرق الرئيسية لرسم الدوال.
IV. دراسة اتجاه التغير : تعيين المجالات التي تكون فيها الدالة متزايدة تماما، متناقصة تماما أو ثابتة
2- جدول التغيرات :
هو جدول نلخص فيه كل المعطيات عن الدوال كمجموعة التعريف واتجاه التغير والصور والسوابق والقيم الحدية .. الخ
مثال : جدول التغيرات التالي يلخص المنحنى المقابل الممثل للدالة `f`
* الفرق بين متزايدة ومتزايدة تماما
مثال
- - الدالة `g` متزايدة تماما على المجال `[-3;0]`
- - الدالة `g` ثابتة على المجال `[0;2]`
- - الدالة `g` متزايدة تماما على المجال `[2;3]`
* لكن على المجال `[-3;3]` نقول فقط أن الدالة `g` متزايدة
نفس المفهوم بالنسبة لمتناقصة ومتناقصة تماما.
V- القيم الحدية :
1- القيم الحدية العظمى :
هي أكبر صورة `f(a)` تبلغها `f` عند سابقة `a` من `D_f`
نعبر عليها وفق المثال بثلاث صيغ فنقول :
- القيمة الحدية الكبرى للدالة `f` هي `(5;7)`
- أو القيمة الحدية الكبرى للدالة `f` هي 7 عند 5
- أو القيمة الحدية الكبرى للدالة `f` هي `f(5)=7`
2- القيمة الحدية الصغرى :
هي أصغر صورة `f(b)` تبلغها `f` عند سابقة `b` من `D_f`
نعبر عليها وفق المثال بثلاث صيغ فنقول :
- القيمة الحدية الصغرى للدالة `f` هي `(3;1)`
- أو القيمة الحدية الصغرى للدالة `f` هي 1 عند 3
- أو القيمة الحدية الصغرى للدالة `f` هي : `f(3)=1`
* ملاحظة :
- يمكن للدالة أن تبلغ قيمتها العظمى أو الصغرى على مجال عند أكثر من عنصر من هذا المجال
- القيم الحدية دائما تكون عددا حقيقيا ( بمعنى `- infty` و `+infty` لا يمكن أن يكونا قيم حدية)
VI- شفعية الدالة (أي زوجية أو فردية أم لا زوجية لا فردية)
1 - حسابيا :
3- الدالة لا زوجية لا فردية :
هي الدالة التي لا يمكن كتابتها على الشكل : `f(-x)=f(x)` ولا على الشكل : `f(-x)=-f(x)` ومنحناها غير متناظر بالنسبة لمحور التراتيب ولا بالنسبة للمبدأ
- ملاحظة : للبرهان أن دالة ما لا زوجية ولا فردية يكفي إيجاد عنصر `a` من `D_f` بحيث : `f(-a) ne f(a)` و `f(-a) ne -f(a)` أو إثبات أن `D_f` غير متناظرة بالنسبة إلى 0
VII- حل معادلات ومتراجحات بيانيا :
`f(x) = g(x) ` `Leftarrow` فواصل نقط تقاطع `C_f ` مع `C_g`
`f(x) > g(x) ` `Leftarrow` المجال من `x` أين يكون `C_f` فوق `C_g`
`f(x) < g(x) ` `Leftarrow` المجال من `x` أين يكون `C_f` تحت `C_g`
مثال :
`D_f=[-3;4] ` و `D_g=[-2,5;2,5]`
`f(x) =g(x) Rightarrow x in {-2;1}`
`f(x) ge g(x) Rightarrow x in [-2;1]`
`f(x) gt g(x) Rightarrow x in ]-2;1[`
`f(x) le g(x) Rightarrow x in [-3;-2] cup [1;4]`
`f(x) lt g(x) Rightarrow x in ]-3;-2[ cup ]1;4[`
`f(x)=1 Rightarrow x in {-2;0;4}`
`f(x) ge 1 Rightarrow x in [-2;0]`
`f(x) lt 1 Rightarrow x in [-3; -2[ cup ]0; 4]`
`g(x)=1 Rightarrow x in {-2;2}`
`g(x) lt 1 Rightarrow x in [-2,5; -2[ cup ]2;2,5]`
`g(x) le 1 Rightarrow x in [-2;2]`
`f(x) = -3 Rightarrow x=2`
`g(x)=-3 Rightarrow x=0`
* نرمز للمجموعة الخالية بالرمز `\emptyset` أو بالرمز `{}`
`f(x) ge -3 Rightarrow x in [-3;4]`
`g(x) gt -3 Rightarrow x in [-2,5; 0[ cup ]0; 2,5]`
`f(x) le -3 Rightarrow x=2`
`g(x) lt -3 Rightarrow S= \emptyset`
`f(x) ge 3 Rightarrow S=\emptyset`
`g(x) le -4 Rightarrow S=\emptyset `
`f(x) ge 3 Rightarrow S=\emptyset`
`g(x) le -4 Rightarrow S=\emptyset `
VIII- إشارة الدالة
1- حسابيا :
`f` موجبة `f(x) gt 0 Leftarrow`
`f` سالبة `f(x) lt 0 Leftarrow`
`f` معدومة `f(x) = 0 Leftarrow`
2- بيانيا
`f` موجبة `C_f` فوق محور الفواصل
`f` سالبة `C_f` تحت محور الفواصل
`f` معدومة `C_f` يقطع محور الفواصل
IX- تقاطع دالة مع محور الأحداثيات :
* `C_f` يقطع محور الفواصل `f(x) =0 Leftarrow`
* `C_f` يقطع محور التراتيب `x =0 Leftarrow`











ليست هناك تعليقات:
إرسال تعليق